Fragenliste von Zufallsvariablen
|
Bei einem Glücksspiel können Sie eine von drei Türen wählen. Nr. 3738
|
|
|---|---|
| Lösungsweg | |
|
Bei einem Glücksspiel können Sie eine von drei Türen wählen.
Nr. 3739
|
|
|---|---|
| Lösungsweg | |
|
Bei einem Glücksspiel können Sie eine von drei Türen wählen. Nr. 3740
|
|
|---|---|
| Lösungsweg | |
|
Bei einem Glücksspiel können Sie eine von drei Türen wählen. Nr. 3741
|
|
|---|---|
| Lösungsweg | |
|
„Mensch ärgere dich nicht“: Max hat keine Figur auf dem Spielfeld und darf 3 Mal würfeln. Wenn der Würfel die Augenzahl 6 hat, so kann Max eine Figur aufs Spielfeld bringen. Nr. 3742
|
|
|---|---|
| Lösungsweg | |
|
Roulette: Beim Roulette gibt es 18 rote Felder, 18 schwarze Felder und die Null. Ein Spieler setzt auf rot. Rollt die Kugel auf rot, so erhält der Spieler einen Gewinn in der Höhe seines Einsatzes (und sein Einsatz bleibt ihm erhalten), andernfalls verliert er seinen Einsatz.  Nr. 3743
|
|
|---|---|
| Lösungsweg | |
|
Roulette: Beim Roulette gibt es 18 rote Felder, 18 schwarze Felder und die Null. Ein Spieler setzt auf rot. Rollt die Kugel auf rot, so erhält der Spieler einen Gewinn in der Höhe seines Einsatzes (und sein Einsatz bleibt ihm erhalten), andernfalls verliert er seinen Einsatz.  Nr. 3744
|
|
|---|---|
| Lösungsweg | |
|
Roulette: Beim Roulette gibt es 18 rote Felder, 18 schwarze Felder und die Null. Ein Spieler setzt auf rot. Rollt die Kugel auf rot, so erhält der Spieler einen Gewinn in der Höhe seines Einsatzes (und sein Einsatz bleibt ihm erhalten), andernfalls verliert er seinen Einsatz. Wie hoch ist der erwartete Gewinn, wenn der Spieler in hundert Runden 1 € setzt?  Nr. 3745
|
|
|---|---|
| Lösungsweg | |
|
Zwei Würfel werden geworfen. Untersuchen Sie, ob die folgenden Ereignisse unabhängig sind. Nr. 3746
|
|
|---|---|
|
Zwei faire Würfel werden geworfen. Untersuchen Sie, ob die folgenden Ereignisse unabhängig sind. Nr. 3747
|
|
|---|---|
|
Es werden zwei (faire) Würfel geworfen. Untersuchen Sie, ob die folgenden Ereignisse unabhängig sind. Nr. 3748
|
|
|---|---|
|
Bei einem Glücksspiel erhalten Sie in jedem Durchgang entweder 5, 25, oder 30 Punkte. Wie viele Punkte erhalten Sie im Durchschnitt wenn Sie sehr oft spielen? Nr. 3774
|
|
|---|---|
| Lösungsweg | |
|
Bei einem Glücksspiel erhalten Sie entweder 10, 20, oder 80 Punkte. Nr. 3775
|
|
|---|---|
| Lösungsweg | |
|
Bei einem Glücksspiel können Sie eine von drei Türen wählen. Nr. 3776
|
|
|---|---|
| Lösungsweg | |
|
Bei einem Glücksspiel können Sie eine von drei Türen wählen. Nr. 3777
|
|
|---|---|
| Lösungsweg | |
|
Roulette: Beim Roulette gibt es 18 rote Felder, 18 schwarze Felder und die Null. Ein Spieler setzt auf rot. Rollt die Kugel auf rot, so erhält der Spieler einen Gewinn in der Höhe seines Einsatzes (und sein Einsatz bleibt ihm erhalten), andernfalls verliert er seinen Einsatz.  Nr. 3778
|
|
|---|---|
| Lösungsweg | |
|
Roulette: Beim Roulette gibt es 18 rote Felder, 18 schwarze Felder und die Null. Ein Spieler setzt auf rot. Rollt die Kugel auf rot, so erhält der Spieler einen Gewinn in der Höhe seines Einsatzes (und sein Einsatz bleibt ihm erhalten), andernfalls verliert er seinen Einsatz.  Nr. 3779
|
|
|---|---|
| Lösungsweg | |
|
test Nr. 4047
|
|
|---|---|
| Lösungsweg | |
|
Sei X eine Zufallsvariable, die die Werte 0; 1; 2 und 3 mit den Wahrscheinlichkeiten 1/8; 3/8; 2/8 und 1/8 annimmt. Sind das bereits alle Werte, die X annehmen kann? Nr. 4548
|
|
|---|---|
| Lösungsweg | |
|
Wahr oder falsch: Die Zufallsvariable X = "Augensumme dreier Würfel" ist stetig. Nr. 4549
|
|
|---|---|
| Lösungsweg | |
|
Sei X die Zufallsvariable "Augensumme dreier Würfel". Die Verteilungsfunktion F(x) von X gibt dann die Wahrscheinlichkeit an, dass eine Augensumme X gewürfelt wird, für welche gilt: Nr. 4550
|
|
|---|---|
| Lösungsweg | |
|
Sei X die Zufallsvariable "Augensumme dreier Würfel". Bestimmen Sie P(X=4), also die Wahrscheinlichkeit des Ereignisses "Augensumme ist 4"! Nr. 4551
|
|
|---|---|
| Lösungsweg | |
|
Sei X die Zufallsvariable "Augensumme dreier Würfel". Bestimmen Sie \(P(X \leq 6)\), also die Wahrscheinlichkeit des Ereignisses "Augensumme ist kleiner oder gleich 6"! Nr. 4552
|
|
|---|---|
| Lösungsweg | |
|
Sei X die Zufallsvariable "Augensumme dreier Würfel". Bestimmen Sie P(X>16), also die Wahrscheinlichkeit des Ereignisses "Augensumme ist größer 16"! Nr. 4553
|
|
|---|---|
| Lösungsweg | |
|
Sei X die Zufallsvariable "Augensumme dreier Würfel". Bestimmen Sie \(P(4 Nr. 4554
|
|
|---|---|
| Lösungsweg | |
|
Sei X die Zufallsvariable "Augensumme dreier Würfel". Seien die beiden Werte der Verteilungsfunktion \(F(4) = \frac{4}{216}\) und \(F(6) = \frac{20}{216}\) bekannt. Bestimmen Sie daraus \(P(4 Nr. 4555
|
|
|---|---|
| Lösungsweg | |
|
Sei X die Zufallsvariable "Augensumme dreier Würfel". Bestimmen Sie die Wahrscheinlichkeit P(X=20) und den Wert der Verteilungsfunktion F(20)! Nr. 4556
|
|
|---|---|
| Lösungsweg | |
|
Sei X die Zufallsvariable "Augensumme dreier Würfel" und F(x) ihre Verteilungsfunktion. Wie kann man die Wahrscheinlichkeit angeben für das Ereignis, dass eine zweistellige Augensumme gewürfelt wird? Nr. 4557
|
|
|---|---|
| Lösungsweg | |
|
Für diskrete Zufallsvariablen hat die Verteilungsfunktion immer die Form Nr. 4558
|
|
|---|---|
| Lösungsweg | |
|
Sei X die Anzahl der Würfe mit einem fairen Würfel, bis zum ersten Mal eine Sechs geworfen wird. Welche Werte kann die Zufallsvariable X annehmen? Nr. 4559
|
|
|---|---|
| Lösungsweg | |
|
Sei X die Anzahl der Würfe mit einem fairen Würfel, bis zum ersten Mal eine Sechs geworfen wird. Geben Sie die Wahrscheinlichkeitsverteilung der Zufallsvariablen X an! Nr. 4560
|
|
|---|---|
| Lösungsweg | |
|
Sei X die Anzahl der Würfe mit einem fairen Würfel, bis zum ersten Mal eine Sechs geworfen wird. Wie groß ist die Wahrscheinlichkeit, höchstens 4 Würfe zu brauchen, bis zum ersten Mal eine Sechs gewürfelt wird? Nr. 4561
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei eine stetige Zufallsvariable X, die im Intervall [0;6] gleichverteilt ist. Bestimmen Sie die Dichtefunktion f(x) im Bereich \(0 \leq x \leq 6\) Nr. 4562
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei eine stetige Zufallsvariable X, die im Intervall [0;6] gleichverteilt ist. Bestimmen Sie die Verteilungsfunktion F(x) im Bereich 0<x<6! Nr. 4563
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei eine stetige Zufallsvariable X, die im Intervall [0;6] gleichverteilt ist. Bestimmen Sie die Wahrscheinlichkeit, dass X einen Wert zwischen 0,2 und 0,5 annimmt! Nr. 4565
|
|
|---|---|
| Lösungsweg | |
|
Auf einem Jahrmarkt wird ein Glücksspiel angeboten: Für einen Einsatz von 1 Euro werfen Sie drei faire Würfel gleichzeitig. Bei einer Augensumme von 3 oder 18 erhalten Sie jeweils 100 Euro, ansonsten ist der Einsatz weg. Welche Aussagen sind korrekt? Nr. 4566
|
|
|---|---|
| Lösungsweg | |
|
Ein Bus fährt pünktlich alle 15 Minuten. Sei X die Zufallsvariable, welche durch die Wartezeit in Minuten bestimmt wird, wenn man zufällig zur Bushaltestelle kommt. Welche Aussagen sind korrekt? Nr. 4570
|
|
|---|---|
| Lösungsweg | |
|
Ein Bus fährt pünktlich alle 15 Minuten. Sei X die Zufallsvariable, welche durch die Wartezeit in Minuten bestimmt wird, wenn man zufällig zur Bushaltestelle kommt. Wie ist dann die Wahrscheinlichkeitsdichte definiert? Nr. 4571
|
|
|---|---|
| Lösungsweg | |
|
Ein Bus fährt pünktlich alle 15 Minuten. Sei X die Zufallsvariable, welche durch die Wartezeit in Minuten bestimmt wird, wenn man zufällig zur Haltestelle kommt. Wie groß ist die Wahrscheinlichkeit, dass man höchstens 5 Minuten auf den Bus warten muss? Nr. 4572
|
|
|---|---|
| Lösungsweg | |
|
Ein Bus fährt pünktlich alle 15 Minuten. Sei X die Zufallsvariable, welche durch die Wartezeit in Minuten bestimmt wird, wenn man zufällig zur Haltestelle kommt. Wie groß ist die Wahrscheinlichkeit, dass man mindestens 10 Minuten auf den Bus warten muss? Nr. 4573
|
|
|---|---|
| Lösungsweg | |
|
Ein Bus fährt pünktlich alle 15 Minuten. Sei X die Zufallsvariable, welche durch die Wartezeit in Minuten bestimmt wird, wenn man zufällig zur Haltestelle kommt. Wie lange wird man im Schnitt auf den Bus warten müssen? Nr. 4574
|
|
|---|---|
| Lösungsweg | |
|
Sei X eine stetige Zufallsvariable. Welche Ausssagen sind (unter gewissen Voraussetzungen) korrekt? Nr. 4575
|
|
|---|---|
| Lösungsweg | |
|
Ein Bauteil habe eine Lebensdauer in Jahren, welche definiert ist durch die Verteilungsfunktion \(F(x) = 1-e^{-3x}\) für \(x \geq 0\) und F(x) = 0 sonst. Mit welcher Wahrscheinlichkeit beträgt die Lebensdauer des Bauteils höchstens 1 Jahr? Nr. 4576
|
|
|---|---|
| Lösungsweg | |
|
Ein Bauteil habe eine Lebensdauer in Jahren, welche definiert ist durch die Verteilungsfunktion \(F(x) = 1-e^{-3x}\) für \(x \geq 0\) und F(x) = 0 sonst. Mit welcher Wahrscheinlichkeit beträgt die Lebensdauer des Bauteils 3 bis 6 Monate? Nr. 4577
|
|
|---|---|
| Lösungsweg | |
|
Ein Bauteil habe eine Lebensdauer in Jahren, welche definiert ist durch die Verteilungsfunktion \(F(x) = 1-e^{-3x}\) für \(x \geq 0\) und F(x) = 0 sonst. Mit welcher Wahrscheinlichkeit hält das Bauteil länger als 2 Jahre? Nr. 4578
|
|
|---|---|
| Lösungsweg | |
|
Ein Bauteil habe eine Lebensdauer in Jahren, welche definiert ist durch die Verteilungsfunktion \(F(x) = 1-e^{-3x}\) für \(x \geq 0\) und F(x) = 0 sonst. Nach welcher Zeit ist das Bauteil mit 50%-iger Wahrscheinlichkeit ausgefallen? Nr. 4579
|
|
|---|---|
| Lösungsweg | |
|
Beim Wurf dreier Würfel sind die drei Zufallsvariablen \(X_i = Augenzahl \; des \; i-ten \; Wuerfels \;\; (i=1,2,3) \) Nr. 4580
|
|
|---|---|
| Lösungsweg | |
|
Wahr oder falsch: Der Erwartungswert gewichtet alle Werte einer Zufallsvariablen X gleich. Nr. 4581
|
|
|---|---|
| Lösungsweg | |
|
Berechnen Sie den Erwartungswert der Zufallsvariablen X = Anzahl Köpfe beim Wurf dreier Münzen! Nr. 4582
|
|
|---|---|
| Lösungsweg | |
|
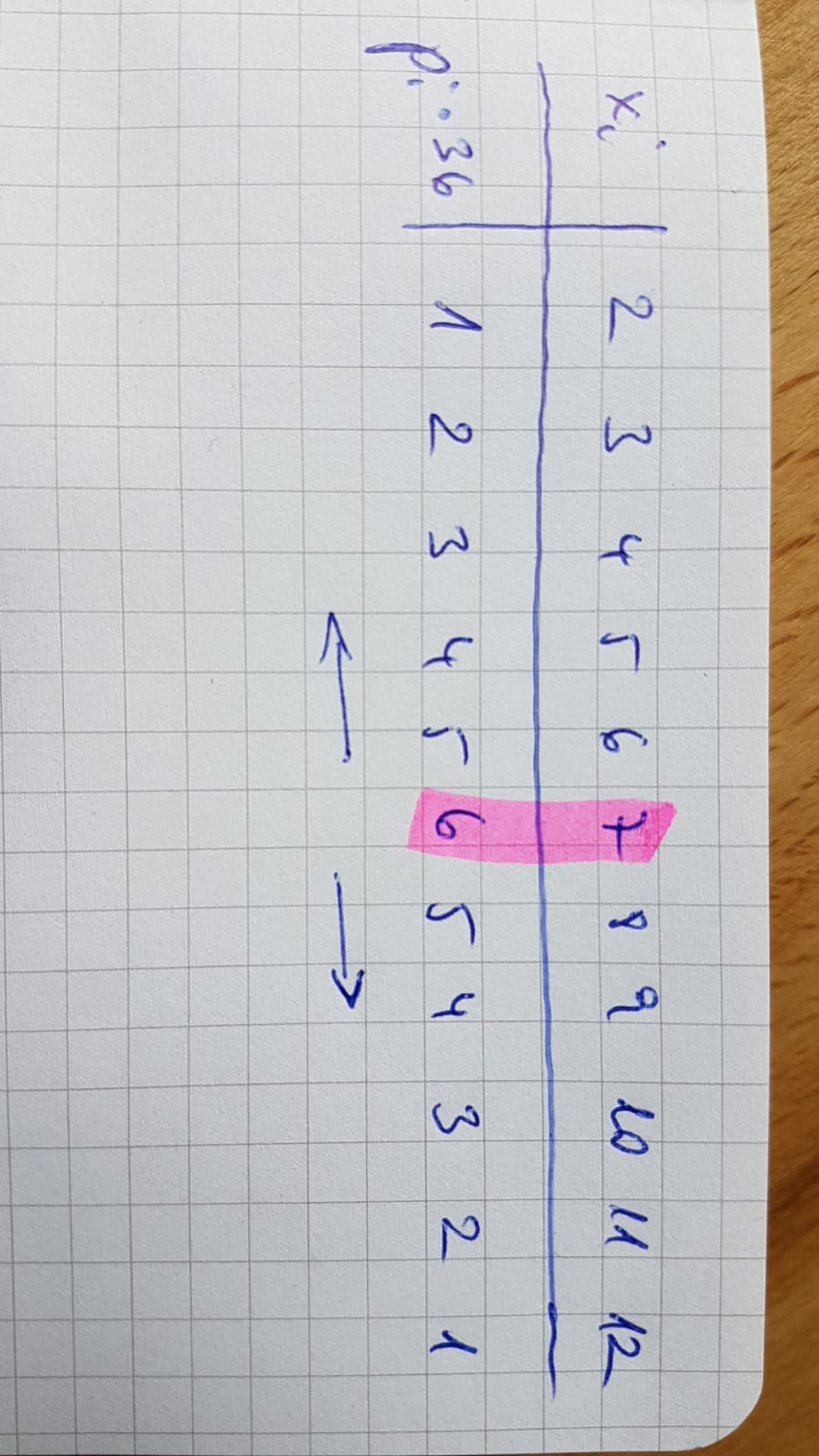
Bestimmen Sie den Erwartungswert der Zufallsvariablen X = Augensumme beim Wurf zweier fairer Würfel! (Tipp: Betrachten Sie zunächst die Augensumme beim Wurf eines Würfels.) Nr. 4583
|
|
|---|---|
| Lösungsweg | |
|
Der Erwartungswert der Zufallsvariablen X = "Anzahl der Köpfe beim Wurf einer Münze" beträgt E(X) = 0,5. Berechnen Sie daraus den Erwartungswert der Zufallsvariablen Y = "Anzahl der Köpfe beim Wurf dreier Münzen"! (Annahme: Alle Münzen sind fair.) Nr. 4584
|
|
|---|---|
| Lösungsweg | |
|
Die Varianz der Zufallsvariablen X = "Anzahl der Köpfe beim Wurf einer Münze" beträgt Var(X) = 0,25. Berechnen Sie daraus die Varianz der Zufallsvariablen Y = "Anzahl der Köpfe beim Wurf dreier Münzen"! (Annahme: Alle Münzen sind fair.) Nr. 4585
|
|
|---|---|
| Lösungsweg | |
|
Bei einer Produktionsanlage treten Störungen mit folgender Verteilung für die Zufallsvariable X = Anzahl der Störfälle pro Tag auf: P(X=0) = 0,3; P(X=1) = 0,4; P(X=2) = 0,2 und P(X=3) = 0,1. Die Kosten für die Behebung einer Störung betragen 1000 Euro pro Störfall. Welche Kosten sind im Schnitt pro Tag zu erwarten? Nr. 4586
|
|
|---|---|
| Lösungsweg | |
|
Wann ist der Erwartungswert des Produkts zweier Zufallsvariablen gleich dem Produkt der Erwartungswerte, d.h. wann gilt \(E(X \cdot Y)= E(X) \cdot E(Y)\)? Nr. 4587
|
|
|---|---|
| Lösungsweg | |
|
Wann ist der Erwartungswert der Summe zweier Zufallsvariablen gleich der Summe der Erwartungswerte, d.h. wann gilt E(X+Y)= E(X)+E(Y)? Nr. 4588
|
|
|---|---|
| Lösungsweg | |
|
Seien X und Y zwei Zufallsvariable und Cov(X;Y) ihre Kovarianz. Welche Aussagen sind wahr? Nr. 4589
|
|
|---|---|
| Lösungsweg | |
|
Gegeben sei die Zufallsvariable X = Anzahl der Köpfe beim Wurf dreier Münzen. Es gilt E(X) = 1,5 und Var(X) = 0,75. Schätzen Sie P(|X-1,5| < 1) (also die Wahrscheinlichkeit, dass die Anzahl der Köpfe um weniger als 1 vom Erwartungswert 1,5 abweicht) mit der Ungleichung von Tschebyscheff ab, und berechnen Sie P(|X-1,5| < 1) exakt! Nr. 4590
|
|
|---|---|
| Lösungsweg | |
|
Was besagt das Gesetz der großen Zahlen? Nr. 4591
|
|
|---|---|
| Lösungsweg | |
|
Sie entnehmen zufällig (ohne Zurücklegen) 4 Kugeln aus einer Urne mit 6 roten und 18 blauen Kugeln. Wie groß ist die Wahrscheinlichkeit, dass Sie genau eine rote Kugel ziehen? Wie viele rote Kugeln sind im Schnitt in Ihrer Stichprobe zu erwarten? (Tipp: Überlegen Sie, um welche Verteilung es sich handelt, und nutzen Sie die entsprechende Formel für den Erwartungswert!) Nr. 4592
|
|
|---|---|
| Lösungsweg | |
|
In einer Fabrik wird ein Bauteil produziert, der Anteil fehlerhafter Teile ist dabei konstant. Es wird eine zufällige Stichprobe von n Bauteilen entnommen. Welche Wahrscheinlichkeitsverteilung hat die Zufallsvariable X = Anzahl fehlerhafter Bauteile in der Stichprobe? Nr. 4593
|
|
|---|---|
| Lösungsweg | |
|
Eine Fertigungsanlage hat einen gleichbleibenden Ausschuss-Anteil von 0,5%. Mit welcher Wahrscheinlichkeit findet man unter 100 entnommenen Produktionseinheiten höchstens ein fehlerhaftes? Berechnen Sie die Lösung exakt sowie als Näherung durch die Poisson-Verteilung! Nr. 4594
|
|
|---|---|
| Lösungsweg | |
|
Bei der Übertragung von Vierer-Bitfolgen kommt es mit einer Wahrscheinlichkeit von 0,5% zu Übertragungsfehlern. Sei X die Zufallsvariable "Anzahl der Bitfehler in einer zufällig gesendeten Bitfolge der Länge 4". Wie groß ist die Wahrscheinlichkeit, dass mindestens ein Bitfehler auftritt? Wie viele Fehler sind im Schnitt pro gesendeter Bitfolge zu erwarten? Nr. 4595
|
|
|---|---|
| Lösungsweg | |
|
Beim telefonischen Support-Dienst eines Herstellers treffen zur Hauptgeschäftszeit pro Stunde im Schnitt 240 Anrufe ein. Wie groß ist die Wahrscheinlichkeit, dass innerhalb von einer Minute kein Anruf bzw. mehr als 5 Anrufe eintreffen? (Annahme: Die Anzahl der Anrufe ist poissonverteilt.) Nr. 4596
|
|
|---|---|
| Lösungsweg | |
|
Bei Marmeladengläsern ist das Abfüllgewicht normalverteilt mit \(\mu\) = 200 Gramm und \(\sigma\) = 5 Gramm. Legen Sie den Toleranzbereich \([\mu -c;\;\; \mu +c]\) fest, in den 90% aller Abfüllgewichte fallen! Nr. 4600
|
|
|---|---|
| Lösungsweg | |
|
Seien X und Y zwei normalverteilte Zufallsvariable. Dann ist ihre Summe X+Y Nr. 4601
|
|
|---|---|
| Lösungsweg | |
|
Was sagt der zentrale Grenzwertsatz über die Summe \(X = X_1 + ... + X_n\) von n unabhängigen und identisch verteilten Zufallsvariablen \(X_1, ..., X_n\)? Nr. 4602
|
|
|---|---|
| Lösungsweg | |
|
Bei einer Zufallsstichprobe sind die Stichprobenvariablen Nr. 4605
|
|
|---|---|
| Lösungsweg | |
NEWS
Derzeit kommt es beim Rendern der Formeln leider zu einem Problem. Wir sind bemüht das Problem zu lösen.
Auch in diesem Semester für alle FHTW Studierenen wieder verfügbar: Der Mathe-Support
Mathematik lernen ist eine Herausforderung, vor allem im Eigenstudium! Sie tun sich schwer beim Lesen von mathematischen Skripten oder kommen bei den Übungsaufgaben nicht weiter? Vielleicht wollen Sie auch einfach nicht alleine, sondern lieber in einer Gruppe lernen? Dann kommen Sie zum Mathe-Support!
Die Mathe Plattform des Technikum Wien gewinnt den eLearning Award 2019 als Projekt des Jahres in der Kategorie Hochschule.
Festigen Sie Ihre Grundkenntnisse und bereiten Sie sich auf Prüfungen vor.
Im Juli starten wieder die Warm-up Kurse - ein kostenloser Service für Aufgenommene und Studierende der FHTW.
Mathematik, Physik, Elektrotechnik, Informatik, Englisch und Deutsch in kompakten Kursen, geblockt bis September.
Anmeldung und Informationen
Warm-up-Kurse
Die Plattform wächst! Wir bauen im Moment den Bereich des Studienwissens aus. Bitte haben Sie Verständnis, dass die Inhalte dort erst nach und nach ergänzt werden. Ebenso kann es bei Design und Grafik noch zu Änderungen, Verbesserungen und kleinen Bugs kommen. Danke für Ihr Verständnis!